数学でよく使用する円周率πですがみなさんはどのように計算しているでしょうか。
関数電卓には実装されていますが、キーボードでπを打っても
文字として認識されるため、計算することができません。
そこで今回は円周率πを関数を使用して計算する方法を紹介したいとおもいます。
それでは見ていきましょう。
⬛︎こんな事ができるようになる!
円周率πを「3.141592…」と打ち込まなくても
「3.14159265358979」の円周率πの15桁を関数を使用して
出力・計算できるようになる

⬛︎関数の仕組み
使用する関数はPI関数となります。
=PI()
引数はなく、「=PI()」だけで成り立つ関数になります。
「PI()」=「円周率πの近似値」という意味です。
⬛︎関数の使用方法
では本題です。
ここからは関数の使用方法から実用例を紹介したいと思います。
・円周率πを出力
まずは円周率πをセルに出力・表示してみましょう。
今回は例でB3に表示したいと思います。
関数の使用方法は「=PI()」でしたよね。
これをB3に入力するだけです。

結果はこのようになります。

B3に「3.14159265359」が表示されました。
引数がないのでとてもシンプルな関数です。
・PI関数を使用して面積を求める
ではPI関数を用いて計算をしてみましょう。
よく使用される円の面積から求めてみたいと思います。
円の面積を求める公式はこちらです。
円の面積=半径×半径×円周率π
ではこちらを元に計算していきましょう。
今回求めたい円の半径は3とします。
では先ほどの公式に当てはめてみましょう。
=3*3*PI()

入力した結果はこちらです。
面積は「28.274…」という事がわかりました。
・円の周長を求める
今度は円の周長を求めてみましょう。
公式はこのようになります。
円の周長=2×半径×円周率π
今回は半径5の周長を求めてみましょう。
先ほどの公式に当てはめるとこのようになります。
=2*5*PI()

入力した結果はこちらです。

結果は「31.415…」ということがわかりました。
・球の体積を求める
今度は球に移りたいとおもいます。
まず、球の体積から見ていきましょう。
公式はこちらです。
球の体積=4/3×半径×半径×円周率π
今回は半径8の球の体積とします。
先ほどの公式に当てはめるとこのようになります。
=4/3*8*8*PI()

入力した結果はこちらです。

結果は「268.0826」ということがわかりました。
・球の表面積を求める
最後に球の表面積を求めましょう。
球の表面積を求める公式はこちらになります。
球の表面積=4×半径×半径×円周率π
今回は12の球の表面積とします。
先ほどの公式に当てはめるとこのようになります。
=4*12*12*PI()

入力した結果はこちらです。

結果は「1809.557」ということがわかりました。
⬛︎よくあるエラーと対処法
ではPI関数を使用する上でよくあるエラーと対処法について説明します。
・この数式に問題が見つかりました
こちらのエラーは引数を入力している可能性があります。
下図をご覧ください。

PI関数は引数は不要ですが、見本で入力してみました。
結果はこのようになります。
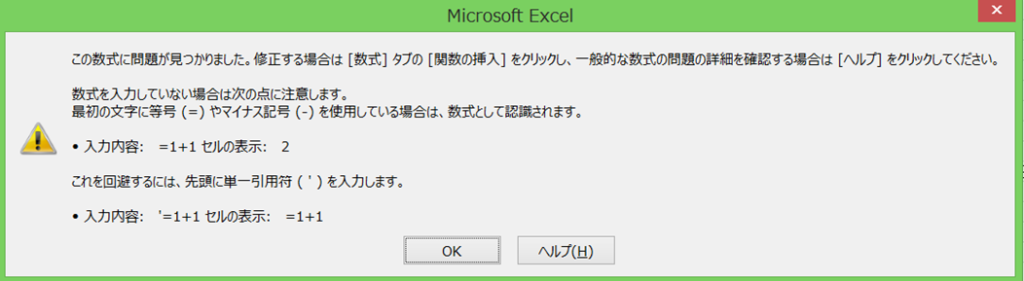
「この数式に問題が見つかりました」というエラーになりました。
PI関数では引数を入力するとエラーになります。
⬛︎公式の説明
わかりやすいように説明するため、公式の語句とはことなる文で説明ましたが
公式の内容については下記リンクをご参照ください☟
⬛︎まとめ
いかがだったでしょうか。
今回は様々な例を用いて説明しましたが
円周率π=「PI()」という事を覚えておけば問題ありません。
もちろん3.14などと入力して計算してもいいですが
PI関数は15桁まであるので、より正確に計算できます。
是非活用してみて下さい。
それでは次回の記事でお会いしましょう。




コメント