標準偏差を使用したことはありますか?
データのばらつきを求める際によく用いられる分析方法です。
統計分析に詳しい方はよく耳にする標準偏差ですが
エクセルでは関数1つで算出することができます。
標準偏差には「母集団」として算出する方法と「サンプル」として算出する方法があります。
まずは標準偏差の主な内容と活用方法、そしてSTDEV.P・STDEV.S関数の違いと
使用方法についてまとめていますので是非参考にしてみてください。
それでは見ていきましょう。
■関数の仕組み
まず関数の仕組みを見てみましょう。
母集団で標準偏差:=STDEV.P(対象データ)
標本で標準偏差:=STDEV.S(対象データ)
■標準偏差とは
まず、標準偏差とは何かについて説明します。
しかし、この記事をご覧になられている方は標準偏差の存在を知っていて
ある程度の知識をお持ちだと思うので簡単に紹介したいと思います。
標準偏差とは、データがどれくらいばらついているか求める統計分析の手法です。
では1例を紹介します。
下図をご覧ください。
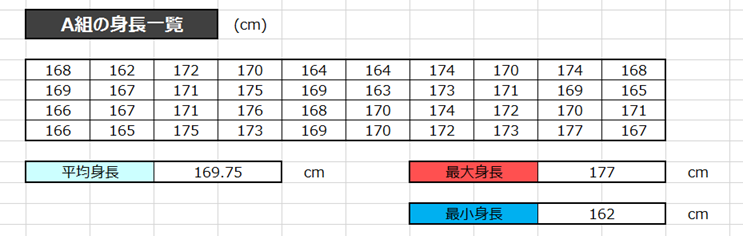
A組の生徒の40人分の身長のデータがあったとします。
身長は162cm~177cmの範囲内に存在するところまではわかりました。
そして平均身長は169.8cmです。
大まかにデータの分布は想像できますが、
「身長のばらつきはどのくらいなの?」と聞かれると明確な回答はできません。
そこで使用するのが「標準偏差」です。
では身長のまとめた結果をグラフに直してみます。
結果は下図のようになりました。
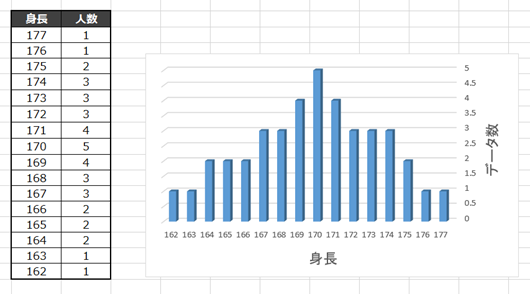
平均値付近はデータ数が多いですが
最小値・最大値に向かうにつれでデータ数も減っていますね。
こちらのグラフを少しなだらかにしてみます。
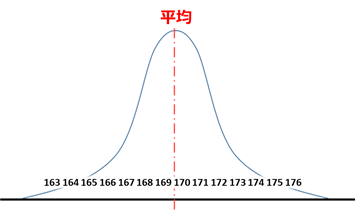
こちらのグラフを「正規分布曲線」といいます。
ここで「標準偏差」を登場させますが、求め方は後回しにして
どのような役割があるのか紹介したいと思います。
まず、標準偏差の記号を「σ(シグマ)」といいます。
母集団だと大文字になるなどの制約は今回は省略したいと思います。
結果からいうと今回の身長の標準偏差は「σ=3.66」です。(求め方は後で説明します)
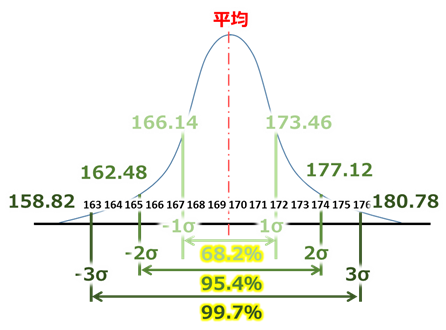
そして正規分布には下記のような法則があります。
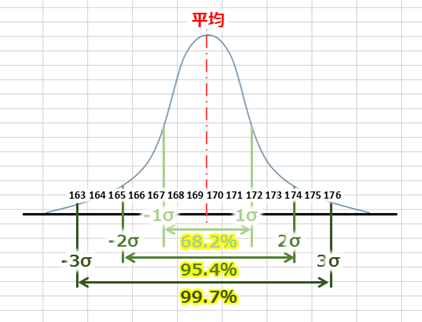
「1σ~-1σ」間は約68.2%のデータ。
「2σ~-2σ」間は約95.4%のデータ。
「3σ~-3σ」間は約99.7%のデータ。
標準偏差σは「3.66」でしたのでそれぞれ計算してみましょう。
たとえば2σだと「平均+2σ」なので「169.8+23.66」=177.12
-3σだと「平均-3σ」なので「169.8-33.66」=158.82となります。
全て計算した結果を下記に示します。
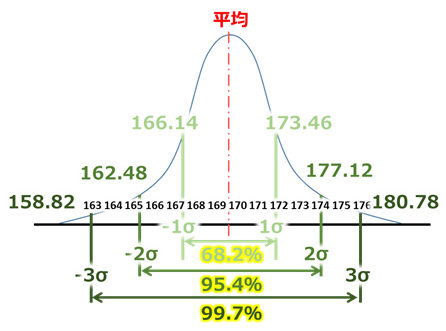
ここから言えることとして、身長は「166.14~173.46」cmの人は68.2%の割合。
身長は「162.48~177.12」cmの人は95.4%の割合。
身長は「158.82~180.78」cmの人は99.7%の割合であることがわかります。
いかがでしたか。統計学は面白いですね。
■STDEV.P・STDEV.S関数の違いについて
ではタイトルのSTDEV.P・STDEV.S関数の違いについて紹介したいと思います。
まずSTDEV.P・STDEV.S関数の説明を見てみましょう。

違いとしてはSTDEV.P関数は「母集団」でSTDEV.S関数は「標本(サンプル)」となります。
では「母集団」と「標本(サンプル)」の違いが分かればどちらを使用すればいいかわかりますね。
母集団はすべてのデータを対象とするのに対し標本は母集団の中から抜き取って計算をします。
先ほどの身長のデータを振り返りましょう。
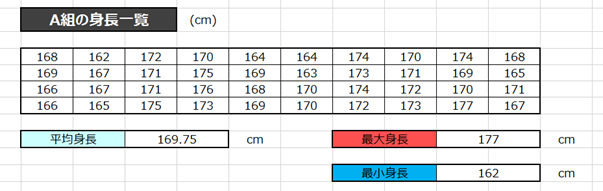
今回は「A組」の生徒の身長データを参照していますよね。
A組の標準偏差を求める場合は40人すべてのデータがあるので
STDEV.P関数の「母集団」で計算しますが
仮にクラス全体の身長の標準偏差を求める場合にA組のみの身長を元データとすると
クラス全員という母集団の中のA組のデータを抜き取って計算することになるため、
STDEV.S関数の「標本(サンプル)」
で計算することになります。
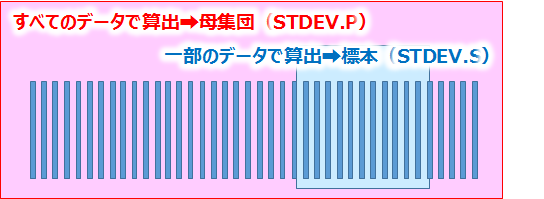
もう1つ事例を紹介したいと思います。
すでに100万個の部品があり、部品の長さの標準偏差を求めたいとします。
100万個すべてデータを集めて標準偏差を計算する場合はSTDEV.P関数の「母集団」
で計算しますが100個のみ抜き取って計算する場合はSTDEV.S関数の「標本(サンプル)」を使用するようになります。
なので使用頻度はSTDEV.S関数の「標本(サンプル)」が多いかと思います。
「標本」のSTDEV.S関数の特徴として、抜き取りのデータから母集団のばらつきを予想するので
標準偏差は母集団で計算したより、標本で計算した方が数値は大きくなります。
■STDEV.P・STDEV.S関数で標準偏差を計算する
それでは実際に関数を使用して計算してみましょう。
本来、標準偏差を計算するには分散など複雑な計算が必要です。
しかしSTDEV.P・STDEV.S関数を使用すれば、簡単に計算できます。
1から計算したことがある方はわかると思いますが、とても簡単で、ありがたい関数です。
では実際に使用してみましょう。
先ほどの身長データを使用してみましょう。
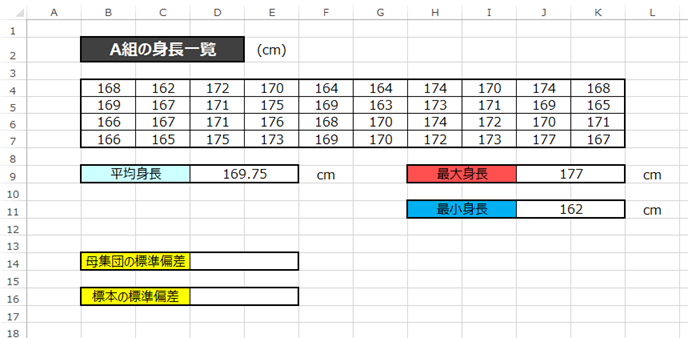
今回は母集団と標本の標準偏差をそれぞれ計算してみましょう。
では関数の仕組みを見てみましょう。
母集団で標準偏差:=STDEV.P(対象データ)
標本で標準偏差:=STDEV.S(対象データ)
対象データは「B4からK7」の40個のデータを参照してみましょう。
では関数に当てはめていきます。
母集団の標準偏差☟
=STDEV.P(B4:K7)
標本の標準偏差☟
=STDEV.S(B4:K7)
では実際に入力してみましょう。
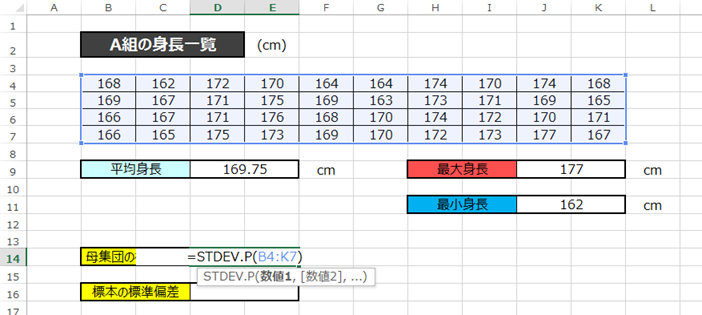
結果はこのようになります。
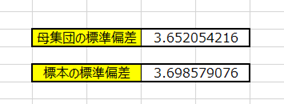
これで標準偏差を計算することができました。
母集団では1σ=3.65ということになりますね。
こちらを活用すると先ほどの範囲を算出できます。
これで関数1つで標準偏差を算出できました。
■よくあるエラーと対処法
それではSTDEV.P・STDEV.S関数を使用する中でよくあるエラーと対処方について説明します。
・対象の数値に文字列のデータがある
こちらはエラーになりませんが、標準偏差の計算に含まれなくなってしまいます。
対象データのセルの左上に緑の印がある場合は要確認です。
下図をご覧ください。

セルを選択して文字列になっている場合は標準または数値に直して
再度入力しなおしてください。
■VBAでの活用方法
VBAを使用しての活用方法も紹介しています。
是非参考にしてみてください。
■公式の説明
わかりやすいように説明したため公式と使用する語句が異なりますが
マイクロソフト公式の説明については下記のリンクを参照してください。☟
■まとめ
いかがだったでしょうか。
標準偏差はデータのばらつきを把握するうえでとても便利な統計手法です。
さらにエクセルを使用すると複雑な計算をしなくても
関数1つで計算可能です。
ぜひ母集団・標本の違いを理解して活用してみてください。
それでは次回の記事でお会いしましょう。




コメント