角度の単位には度(°)で表される度数法と
ラジアン(rad)で表される弧度法が存在します。
お互いメリットデメリットがあり、扇形の弧の長さや面積・微分積分をする際には弧度法に
変換したり、馴染みのある「°」で表記するために度数法に変換したりなど
数学でよく使用する方法です。
そこで今回はラジアンの弧度法から「°」の度数法に変換する方法を紹介します。
対称となる度数法から弧度法への変換方法については下記の記事をご参照ください。
【RADIANS関数】ラジアン(弧度法)を求める!エクセルで度数法から弧度法へ! ► 独学エクセル塾 (dokugakuexcel.com)
具体的な使用例も紹介していますので是非参考にしてみてください。
それではみていきましょう。
⬛︎こんなことができるようになる!
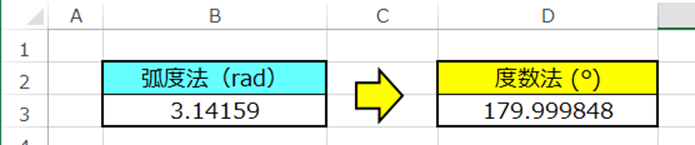
弧度法(ラジアン)から度数法(°)への変換ができるようになる。
⬛︎関数の仕組み
=DEGREES(度数法に変換したいラジアンの数値)※引数はセル参照でも直接入力してもかまいません。
⬛︎弧度法と度数法とは
まず、大まかに弧度法と度数法の違いを紹介します。
弧度法の単位は「ラジアン[rad]」ですが、度数法は「度[°]」になります。
よく目にする度数法の単位は「°」ですよね。
対する弧度法はあまりイメージが付きにくいと思います。
同じ角度でも2種類あるのにも訳があります。
それぞれのメリットを下記にまとめています。
○度数法のメリット
・角度をシンプルに表現できる(弧度法は切りのいい数値にならないため、日常で表現しにくい)○弧度法のメリット
・扇形の弧の長さ・面積が求めやすい
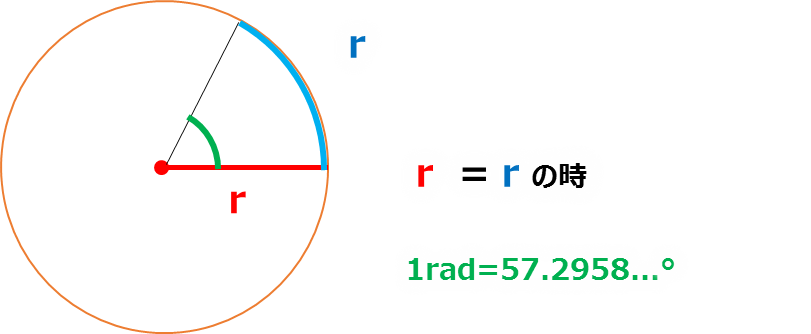
・微分積分の計算が簡潔になる1radは円の半径rと同じ長さの円弧を繋ぎ合わせた際の中心角が1radになります。
参考に1radは角度に直すと「57.2958…°」になります。
度数法と弧度法の関係式はこのようになります。
θ[rad]=θ[°]×180/π
θ°=θ[rad]×π/180
それを主要角度の30°.45°.60°.90°.120°.135°150°.180°で表すと下の表になります。
| 角度 [ ° ] | ラジアン [ rad ] |
|---|---|
| 30° | π/6 |
| 45° | π/4 |
| 60° | π/3 |
| 90° | π/2 |
| 120° | 2π/3 |
| 135° | 3π/4 |
| 150° | 5π/6 |
| 180° | π |
ではDEGREES関数を使用して弧度法から度数法に変換する方法を見ていきましょう。
⬛︎弧度法から度数法へ変換する
では実際に関数を使用して弧度法から度数法に変換してみましょう。
下図の見本をご覧ください。
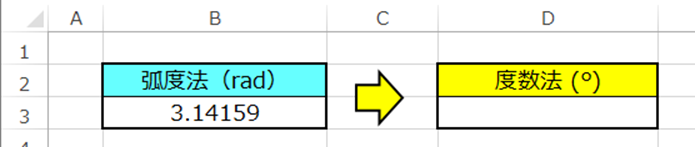
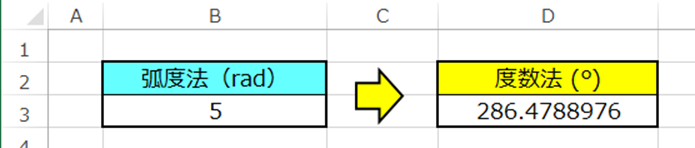
B3にラジアンで入力された数値があります。
今回はこちらの数値を度数法に変換してみましょう。
再度関数の仕組みを確認してみましょう。
=DEGREES(度数法に変換したいラジアンの数値)
ここにB3を参照するとこのようになります。
=DEGREES(B3)
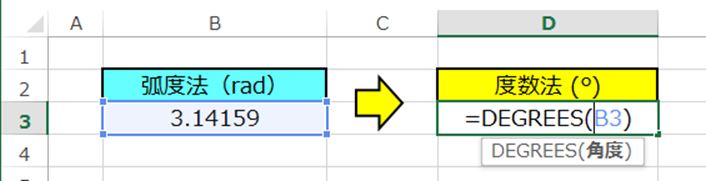
では実行してみましょう。
結果はこのようになります。

数値が「約180°」になりましたね。
つまり「3.14159rad」は「180°」ということがわかりました。
先ほどの表を見ると「Πは180°」なのでうまく変換できていますね。
もちろん、B3の数値を変更してもラジアンから度に変換してくれます。
先ほどは「=DEGREES(B3)」とセルを参照しましたが、
数値を直接入力しても機能してくれます。
例えば「=DEGREES(6.283185307)」と入力してみましょう。
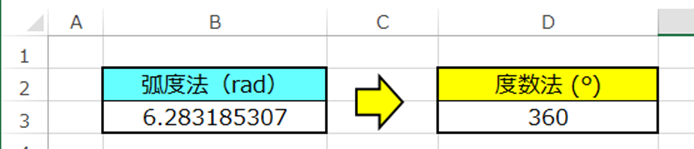
結果は先ほどと同様にラジアンから度に変換してくれました。
■DEGREES関数の応用方法
ではDEGREES関数を応用して角度を求めていきましょう。
・ASINを使用して計算する
例としてASIN関数を紹介します。
今回は45°の直角三角形について見ていきましょう。
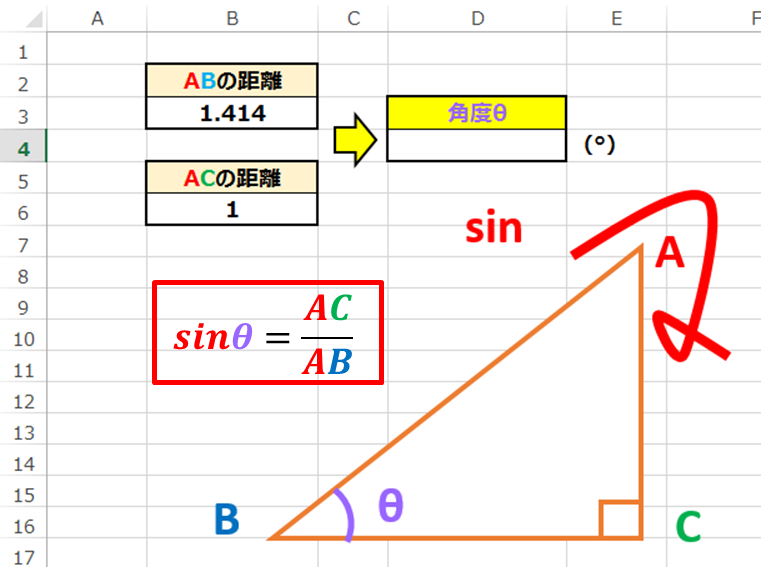
B3に AB間の長さ・B6にAC間の長さが入力されてあります。
関数の使用方法は下記の通りです。
= ASIN(アークサインを求めたい数値・参照したい番地)
これに三角関数の「sinθ=AC /AB」を当てはめるとこのようになります。
=ASIN(B6/B3)
こちらの結果は弧度法のラジアン[rad]なのでDEGREES関数を用いて度数法に変換しましょう。
すると数式はこのようになります。
=DEGREES(ASIN(B6/B3))

では入力してみましょう。
結果はこのようになります。
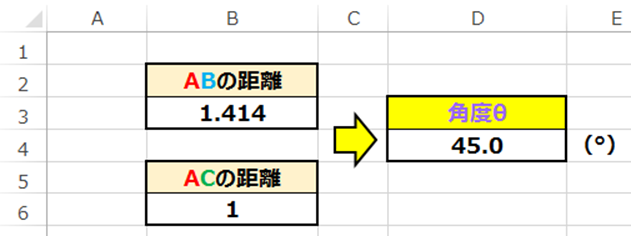
「45」が出力されたため、角度θは「45°」ということがわかりました。
⬛︎よくあるエラーと対処法
ここではDEGREES関数を使用する中で発生するエラーと対処法について紹介します。
・#VALUE!のエラーになる
こちらは参照したセルの内容・引数に入力した値が文字になっている可能性があります。
説明で使用した見本を見てみましょう。
通常であれば弧度法から度数法に変換してくれています。
では参照元のB3の値を文字にしてみましょう。
結果はこのようになります。
結果として#VALUE!のエラーが発生してしまいました。
エラーが発生したら正確に数値を入力しているか確認してみてください。
⬛︎公式の説明
わかりやすいように実際の内容とは異なった語句・文字で説明しています。
公式の内容をご覧になりたい方は下記リンクをご参照ください。
⬛︎まとめ
いかがだったでしょうか。
RADIANS関数とセットで覚えてしまうと弧度法と度数法の換算は
とても簡単になります。
学生の方は答え合わせなどにも使用出来そうですね!
それでは次回の記事でお会いしましょう。




コメント